1. Método de Sustitución
El método de sustitución consiste en aislar en una ecuación una de las dos incógnitas para sustituirla en la otra ecuación.
Este método es aconsejable cuando una de las incógnitas tiene coeficiente 1.
EJEMPLO 1
La solución del sistema es:
2. Método de Reducción
El método de reducción consiste en sumar (o restar) las ecuaciones del sistema para eliminar una de las incógnitas.
Este método es aconsejable cuando una misma incógnita tiene en ambas ecuaciones el mismo coeficiente (restamos las ecuaciones) o los coeficientes son iguales pero con signo opuesto (sumamos las ecuaciones).
Ejemplo 2
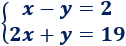
La solución del sistema es
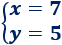
3. Método de Igualación
El método de igualación consiste en aislar una incógnita en las dos ecuaciones para igualarlas.
Este método es aconsejable cuando una misma incógnita es fácil de aislar en ambas ecuaciones.
La solución del sistema es
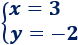
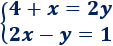
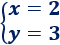
No hay comentarios:
Publicar un comentario