DOMINIO FUNCIONES

Una función es una relación entre dos conjuntos, en la que a cada valor del primer conjunto, denominado dominio, le corresponde un único valor del segundo, denominado recorrido. 

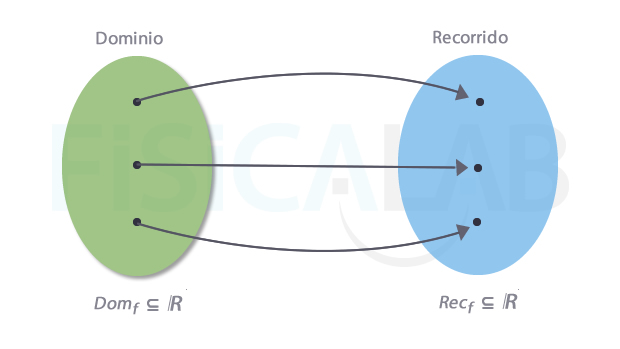
Dominio en funciones reales

Al igual que los dominios de los reyes de la antigüedad marcaban el alcance del poder y la autoridad de los mismos, en el mundo de las funciones, el dominio marca el conjunto de elementos sobre los cuales cada función puede actuar. En una función real de variable real tanto el dominio como el recorrido forman parte del conjunto de los números reales. Cada elemento del dominio se ilustra en la imagen por un punto negro sobre fondo verde, y cada elemento del recorrido como un punto negro sobre fondo azul. Las flechas indican la correspondencia entre unos y otros a través de la función.

El dominio de una función real, también llamado dominio de definición o campo de existencia de la misma, es el conjunto de elementos para los cuales la función está definida. Dicho de otra manera, el subconjunto de los números reales que tienen imagen. Formalmente:

Domf={ x∈R / ∃y=f(x)∈R }

• Domf : Es el dominio de la función. También se puede denotar por Dom(f) o, simplemente, D. Puede ser todo el conjunto de los números reales, o bien un subconjunto de este: Domf⊆R
• x : Es un número real, perteneciente al dominio de la función, que recibe el nombre de variable independiente
• y : Es otro número real, perteneciente al conjunto imagen de la función, que recibe el nombre de variable dependiente. Su valor se obtiene aplicando la función f al valor de x : y=f(x) . Para un par de valores concretos (x,y) decimos que y es la imagen de x, y que x es la antiimagen de y